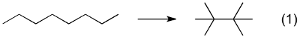2012年5月3日公開
2014年5月20日修正
DFTには分散力や長距離交換の問題など，様々な欠点があることはよく知られてます．このため，例えばn-オクタンから2,2,3,3-テトラメチルブタンへの異性化は，B3LYPなどのポピュラーな汎関数では再現ができません (式1)．
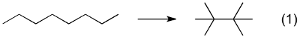
この問題については，いくつかの論文・レビューがすでに出版されてますし，また，筆者は過去に様々な汎関数での異性化エネルギーの計算を行ってきています．
今回は，最近新たに開発されたDFTの分散力補正や，電子相関理論を用いて式1の異性化エネルギーについて計算しました．
まずは，分散力補正なしでのDFT計算の結果を表1に示します．
| 方法 | ΔE [kcal/mol] | 実験値からの絶対値誤差 [kcal/mol] |
|---|---|---|
| 実験値からの見積り | -1.9±0.5 | - |
| BLYP | 9.41 | 11.31 |
| B3LYP | 8.06 | 9.96 |
| revPBE | 9.81 | 11.71 |
| revPBE0 | 8.28 | 10.18 |
| revPBE38 | 7.47 | 9.37 |
| LC-BOP | 4.71 | 6.61 |
| M08-HX | -2.71 | 0.81 |
| PWPB95 | 0.83 | 2.73 |
多数のパラメータを含む，M08-HXのみが実験結果を定性的に再現できました．その他の汎関数はいずれも定性的にも実験値を再現することはできていません．しかしながら，revPBE系の汎関数では，HF交換の比率が高くなる (revPBE, HF 0%; revPBE0, HF 25%; revPBE38, HF 37.5%) と誤差が小さくなる傾向が見られます．また，長距離補正されたLC-BOPでは誤差がさらに小さくなっています．このことから，この問題の原因の一つは，長距離交換にあると考えられます．また，ダブルハイブリット汎関数であり，SOS-MP2相関項が入っているPWPB95では誤差がより小さくなっていることから，DFTでは相関エネルギーの記述も十分ではないと考えられます．
続いて，Grimmeや中井による分散力補正の手法を取り入れた場合の結果を表2に示します．
| 方法 | ΔE [kcal/mol] | 実験値からの絶対値誤差 [kcal/mol] |
|---|---|---|
| 実験値からの見積り | -1.9±0.5 | - |
| BLYP-D3 | 2.53 | 4.43 |
| BLYP-D3(BJ) | 1.38 | 3.28 |
| BLYP-NL | -0.1 | 1.80 |
| B3LYP-D3 | 2.53 | 4.43 |
| B3LYP-D3(BJ) | 1.38 | 3.28 |
| B3LYP-NL | 0.60 | 2.50 |
| revPBE-D3 | 1.57 | 3.47 |
| revPBE-D3(BJ) | 0.76 | 2.66 |
| revPBE-NL | -0.87 | 1.03 |
| revPBE0-D3 | 1.26 | 3.16 |
| revPBE0-D3(BJ) | 0.50 | 2.40 |
| revPBE0-NL | -0.50 | 1.40 |
| revPBE38-D3 | 1.87 | 3.77 |
| revPBE38-D3(BJ) | 0.33 | 2.23 |
| revPBE38-NL | -0.32 | 1.58 |
| LC-BOP+LRD | 0.61 | 2.51 |
| PWPB95-D3(BJ) | -0.81 | 1.09 |
最も精度が高かったのはrevPBE-NLで，1.0 kcal/mol程度の誤差で反応を再現できています．revPBE系の汎関数は，DFT-NLと組み合わせることによって，いずれの場合にも定性的に反応の再現ができています．また，PWPB95-D3(BJ)も1.1 kcal/mol程度の誤差で反応を再現できています．
いずれの分散力補正を用いても誤差は改善されています．Grimmeの分散力補正の場合，誤差はDFT-NL < DFT-D3(BJ) < DFT-D3の順に大きくなっていますが，いずれの場合にも分散力補正がない場合よりも改善された結果を与えています．分散力補正をした場合，全体としては，HF交換の比率に関係なく精度が向上していますが，これは分散力補正が，本質的なDFT汎関数の改良ではなく，DFT計算の結果を後から補正するものであるためと考えられます．
続いて，電子相関理論による異性化エネルギーを表3に示します．
| 方法 | ΔE [kcal/mol] | 実験値からの絶対値誤差 [kcal/mol] |
|---|---|---|
| 実験値からの見積り | -1.9±0.5 | - |
| MP2 | -4.81 | 2.92 |
| SCS-MP2 | -1.30 | 0.60 |
| LPNO-CEPA/1 | -0.22 | 1.68 |
| LPNO-NCPF/1 | -0.20 | 1.70 |
| LPNO-pCCSD/2a | -1.39 | 0.51 |
MP2が2,2,3,3-テトラメチルブタンの安定性を過剰に見積もっている他は，2 kcal/mol以下の精度で見積もれています．特にLPNO-pCCSD/2aとSCS-MP2の精度は高く，分散力補正DFTよりも誤差が小さくなっています．
今回，新たに開発された分散力補正法を用いて，n-オクタンから2,2,3,3-テトラメチルブタンへの異性化について異性化エネルギー (ΔE) を計算しました．DFT-D，DFT-NL，LRDのいずれの分散力補正法も誤差を小さくするという結果でした．Grimmeの分散力補正の場合，DFT-D3 > DFT-D3(BJ) > DFT-NLの順で誤差が小さくなります．
しかしながら，定性的に正しい結果を与えたのは，revPBE系汎関数にDFT-NLを組み合わせた場合，BLYP-NL，PWPB95-D3(BJ)だけであり，最新の分散力補正法を用いても再現が難しいようです．
一方で，電子相関理論を用いた場合，いずれの方法でも精度良く異性化エネルギーを再現することができました．特にLPNO-pCCSD/2aは0.5 kcal/mol程度の誤差で異性化エネルギーを見積もることができており，特筆すべき精度であるといえます．
n-オクタンと2,2,3,3-テトラメチルブタンの構造最適化はTPSS-D3(BJ)/def2-TZVPPレベルで行いました．エネルギー計算ではdef2-QZVP基底関数を用いました．LC-BOPとLC-BOP+LRD以外の汎関数での計算はORCA 2.9.0を用い，RIまたはRI-JKの積分近似を用いました．LC-BOPとLC-BOP+LRDでの計算はGAMESS 2011 R1を使用しました．