DFTによるn-オクタンの異性化エネルギーの見積り

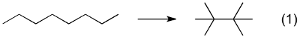
2010年9月5日公開

2014年5月20日修正

はじめに

DFTが苦手な計算の代表にn-オクタンから2,2,3,3-テトラメチルブタンへの異性化が知られています (式1)．様々な論文・レビューがすでに出版されてますが，今回，様々な分散力補正汎関数を含め，実際に計算してみました．

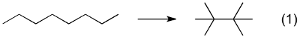
C8H18 → (CH3)3CC(CH3)3

計算結果

表1：n-オクタンの異性化エネルギー (def2-TZVPP基底，構造はPBE/TZV(2d,2p))
方法 ΔE [kcal/mol] 実験値からの絶対値誤差 [kcal/mol]
実験値からの見積り -1.9±0.5 -
BLYP 9.28 11.18
PBE 5.33 7.23
PBEsol 1.62 3.52
BOP 12.21 14.11
BLYP-D -2.87 0.97
BLYP-D3 2.69 4.64
PBE-D -2.26 0.36
B97-D -1.89 0.01
TPSS-D 3.86 1.96
B3LYP 8.07 9.97
B3PW91 7.30 9.20
B97-2 8.37 10.27
B3LYP-D -2.56 0.66
B3PW91-D -3.84 1.94
LC-BOP 4.90 6.80
M06-2X -1.37 0.53
B2PLYP 3.06 4.96
B2PLYP-D -2.51 0.61
B2PLYP-D3 0.08 1.98
B2GP-PLYP-D3 -0.47 1.34
SCS-MP2 -1.76 0.14

分散力補正していない汎関数 ("-D"のついてない汎関数) は軒並み定性的に誤った結果を与えています．分散力補正なしの汎関数で，定性的に正しい結果を与えたのはM06-2X汎関数のみで，長距離補正汎関数のLC-BOPやダブルハイブリット汎関数のB2PLYPも定性的に誤った結果を与えました．

一方で，分散力補正された汎関数 (DFT-D) は非常によい結果を与えていて，B97-Dでは誤差は0.01 kcal/mol，PBE-Dで0.36 kcal/molとなっています．また，B3LYP-D，B2PLYP-Dといった汎関数も0.6 kcal/mol前後の誤差で予測できています．しかしながら，この結果はDFT-Dのsp3混成の炭素原子に対するC6係数が過剰に大きいためであります (See: Grimme, S. Org. Lett.2010, 12, 4670–4673)．このため，その問題が解決されたDFT-D3法ではBLYP-D3，B2PLYP-D3ともに定性的に誤った結果を与えています．一方で，HF項およびPT2項がB2PLYP-D3よりも大きなB2GP-PLYP-D3は定性的に正しい結果を与えており，DFTに根本的な欠陥があります．

また，DFT法ではないSCS-MP2は0.14 kcal/molの誤差で予測できています．

結論

DFTが苦手とするn-オクタンから2,2,3,3-テトラメチルブタンへの異性化についてDFT/def2-TZVPPレベルの計算で異性化エネルギー (ΔE) を計算しました．テストした汎関数の中では，分散力補正されていない汎関数としてはM06-2Xのみが定性的に正しい結果を与えました．

一方で，分散力補正されたDFT (DFT-D) では，いずれの汎関数でも定性的に正しい結果を与えましたが，これはDFT-Dの補正が過剰なためで，間違った理由で一致しているに過ぎません．このため，その問題を解決したDFT-D3では定性的に誤った結果をあたえました．

計算方法

n-オクタンと2,2,3,3-テトラメチルブタンの構造最適化はPBE汎関数とAhlrichsのTZV(2d,2p)基底関数の組み合わせで，Firefly 7.1.Fを用いて行いました．エネルギー計算はBLYP，BLYP-D，B2PLYP，B2PLYP-D，SCS-MP2ではORCA 2.7.0を，BLYP-D3，B2PLYP-D3，B2GPPLYP-D3計算ではORCA 2.8.0を，その他の汎関数の計算ではGAMESS 12 JAN 2009 (R3)を用いました．ORCAでの計算ではRI-JまたはRI-MP2近似を用いました．基底関数にはdef2-TZVPPを用い，ORCAのRI近似では対応する補助基底関数を使用しました．

参考文献

n-オクタンから2,2,3,3-テトラメチルブタンへの異性化について計算した論文・レビューとしては，例えば，以下のようなものがあります．

© 2010-2014 化ケ屋