S…S,S…O,O…O相互作用の理論的研究
はじめに
非結合性の原子間相互作用は,分子のコンフォーメーションや結晶中のパッキングに大きな影響を与えることが知られています.有名なものとしては硫黄同士や硫黄と酸素との相互作用があり,例えばS…O相互作用についてはNagaoらが,X線結晶構造解析とHartree-Fock計算によって検討を行っています
[ref 1].また,タンパク質中におけるS…Y (Y = S, O, N) 相互作用についてはIwaokaとTomodaが,protein databank (PDB) の解析とMP2計算より検討を行っています
[ref 2].これらの結果から,実験と計算の両面において,S…Yの分子間距離はvdW半径の和よりも明確に短くなっていること,SとY原子間に相互作用が存在していることがこれまでに明らかにされています.また,DFT
(B3LYP) 計算によると,2-メトキシヘテロ芳香環において,N…Oの場合には電子対の反発が強く現れるが,O…OやS…Oの場合には反発が生じず,むしろ相互作用が働くという報告もあります
[ref 3].一方,これらの相互作用の要因についてはY原子のローンペアと硫黄—炭素結合のσ*軌道の相互作用,すなわち,nY → σ*S-C相互作用,あるいはY原子のπ軌道との相互作用,πY → σ*S-C相互作用が提案されています [ref 1-3].しかしながら,Sδ+とOδ-との静電的な相互作用であると結論づけた論文もあります[ref 4].そこで本稿では,S…Y相互作用の要因を明らかにするため,図1に示した化合物※を用いて,S…S,S…O,O…Oの相互作用エネルギーを見積もるとともに,NBO解析によってその要因を解析することにしました.

- 図1:モデル分子の構造.X,YはそれぞれSまたはOの任意の組み合わせ.
※以前,pc-chem.infoのblogで取り上げられていた分子が元ネタです.
結果
構造
構造最適化の結果,S…S,S…O,O…Oのすべての組み合わせにおいて,平面構造をとることがわかりました.次に,表1にsyn型構造における,計算で得られたヘテロ原子間の原子間距離とvan
der Walls (vdW) 半径の和をまとめます.
表1:X3LYP/def2-TZVPPで求めたX-Y syn分子内のヘテロ原子 (X, Y) 間距離とvdW半径の和
| ヘテロ原子ペア(X…Y) |
原子間距離 [Å] |
vdW半径の和 [Å, ref 5]
|
差分 [Å] |
| S…S |
3.20 |
3.60 |
0.40 |
| S…O |
2.92 |
3.32 |
0.40 |
| O…O |
2.92 |
3.04 |
0.12 |
いずれの場合においても,vdW半径の和よりもX3LYP/def2-TZVPPレベルの計算で得られた構造における原子間距離の方が短くなっています.特に硫黄を含むペアの場合には0.40
Åも短くなっており,S…Y間において相互作用が働いていることが示唆される結果です.O…Oのペアの場合も若干短くなっていますが,その値は硫黄を含む場合に比べると明確に小さくなっています.また,ベンゾチオフェン-7-カルバルデヒドを例に,nY → σ*S-C相互作用に関連する軌道である,硫黄原子上のσ*,酸素原子上のローンペアのKS(Kohn–Sham)軌道を示します (図2).
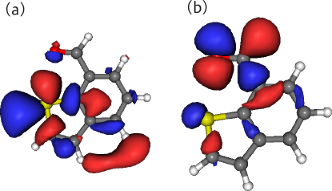
- 図2:ベンゾチオフェン-7-カルバルデヒドのKS軌道.(a) S-C結合の反結合性軌道.(b) アルデヒド酸素上のローンペア
相互作用エネルギー
X3LYP/def2-TZVPPレベルの計算で求めた構造に基づいて,X3LYP/def2-TZVPPまたはSCS-MP2/def2-QZVPPレベルの計算で求めた相互作用エネルギー(全電子エネルギー差,ΔE)を表2にまとめます.
表2:X…Y相互作用エネルギー(全電子エネルギー差,ΔE).構造はX3LYP/def2-TZVPP
| ヘテロ原子ペア(X…Y) |
ΔE, X3LYP/def2-TZVPP [kcal/mol] |
ΔE, SCS-MP2/def2-QZVPP [kcal/mol] |
| S…S |
-1.87 |
-2.23 |
| S…O |
-2.42 |
-2.52 |
| O…O |
0.93 |
0.89 |
硫黄を含むペアの場合には相互作用エネルギーが負になっており,相互作用の結果,安定化していることがわかります.また,相互作用エネルギーはいずれの場合にもX3LYPとSCS-MP2とで同程度の値となりました.この程度の相互作用であればX3LYPで十分に計算できるようです.強いて言うとS…Sの相互作用が弱く評価されていますが,分極率の大きな硫黄原子同士では,相互作用に占める分散力の割合が大きくなるためでしょう.なお,相互作用の強さは,S…Oの方がS…Sよりも強くなっている点が注目すべき点です.
一方で,O…Oのペアではanti体が安定であり,すなわち,ヘテロ原子間に反発力が生じていることが分かります.Coreyらのヘテロ原子を含むエーテルについての論文では
[ref 3],O…Oの系でも反発が生じず,むしろ安定配座とされていますが,これはローンペアが横に並ぶ場合であって,今回のモデル系 (図1) のようにローンペアがちょうど重なり合うような位置に配置されると,有機化学者の直感通りO…Oの系では反発力が生じます.
NBO解析
X3LYP/def2-TZVPPレベルの計算によってNBO解析を行いました.軌道間相互作用として,nY → σ*X-C相互作用に着目し,second-order perturbative estimatesに基づき,Y原子上のローンペアとX-C結合上のσ*軌道とのドナー−アクセプタ相互作用を求めました(表3).
表3:NBO解析によるX-Y syn分子のドナー−アクセプター相互作用解析 (X3LYP/def2-TZVPP)
| ヘテロ原子ペア |
相互作用エネルギー [kcal/mol] |
| S…S |
3.64 |
| S…O |
1.40 |
| O…O |
0.17 |
NBO解析に基づくと,nY → σ*X-C軌道間相互作用の強さはS…S > S…O > O…Oの順になりました.S…Sでは3.64 kcal/molの相互作用がありますが,S…Oになるとかなり弱くなります.さらに,O…Oではほとんど相互作用がなく,軌道間相互作用による安定化はないものとみなしてよいでしょう.
続いて,静電的な相互作用に着目します.静電的な相互作用は,原子上の電荷の大きさによって左右され,より大きな正電荷とより大きな負電荷がより強い相互作用を生じます.そこで,NPA電荷を計算で求めました
(表4).
表4:NBO解析によるX-Ysyn分子のNPA電荷 (X3LYP/def2-TZVPP)
| ヘテロ原子ペア |
X [a.u.] |
Y [a.u.] |
| S…S |
0.477 |
0.031 |
| S…O |
0.477 |
-0.516 |
| O…O |
-0.390 |
-0.498 |
S…Y系では,チオフェン環内の硫黄原子は一定でした.このため,Y原子の電荷によって静電的相互作用の大きさが決定されます.カルボニルやチオカルボニルのヘテロ原子の電荷は,酸素では負,硫黄ではほぼゼロです.電荷の差が大きいほど静電的相互作用の寄与も大きくなるので,静電相互作用の強さはS…O
> S…Sの順になります.O…Oでは,いずれの原子も負電荷を帯びており,負電荷同士の反発力が生じると言えます.
考察
X…Y相互作用エネルギーの大きさはS…O > S…S > O…Oの順であり,XとYの静電的相互作用の強さと一致していることがわかりました.一方で,軌道間相互作用はS…S
> S…O > O…Oの順でした.S…Oの場合は軌道間相互作用が弱く,静電的相互作用が強いことから,S…O相互作用は硫黄原子と酸素原子の間の静電的相互作用によるものであると考えられます.また,SCS-MP2とX3LYPの計算結果がよく一致していることから,分散力の効果は小さいと考えてよいでしょう.一方,S…Sの系では正に帯電した硫黄とほぼ電荷がゼロの硫黄との相互作用になるので,静電的相互作用は考えにくいと言えます.一方で,大きな軌道間相互作用があることから,S…S相互作用の主成分はnS → σ*S–C軌道間相互作用と考えてよさそうです.また,SCS-MP2とX3LYPの計算結果に若干ずれがあることから,分散力の寄与もありそうです.反発力の生じるO…Oの場合,軌道間相互作用はほとんどありません.さらに,酸素原子はいずれも負に帯電しており,O…Oの反発力は主として静電的な反発が原因と考えられます.なお,X-Y anti型で生じるCH…O水素結合による安定化が見積もった反発力に含まれている可能性もあります.いずれにせよ,分子内の軌道間相互作用というのは意外と弱く,クーロン力による静電的相互作用はやはり強い相互作用であるということがわかります.
結論
分子内における,S…S,S…O,O…Oのヘテロ原子間相互佐用をX3LYP/def2-TZVPPレベルの計算で解析すると共に,相互作用エネルギーをSCS-MP2/def2-QZVPPで見積もりました.相互作用エネルギーの強さはS…O
> S…S > O…Oの順であり,S…O,S…Sでは結合的に作用し,O…Oの場合には反発力が生じることがわかりました.X3LYP/def2-TZVPPレベルの計算によるNBO解析の結果,S…O相互作用は弱い軌道間相互作用と強い静電的相互作用が寄与しており,S…Sでは軌道間相互作用が主として働いていることがわかりました.一方,O…Oの場合に反発的になるのは,主として負電荷同士の静電的相互作用が原因であることがわかりました.
計算方法
すべての構造最適化はX3LYP汎関数 [ref 6] とdef2-TZVPP基底関数 [ref 7] を用いて行いました.なお,X3LYP汎関数はよく使われているB3LYP汎関数よりも弱い相互作用の計算に向いていること報告されています [ref 8].得られた構造は振動数解析を行い,平衡構造であることを確認しました.得られた構造を用いたNBO解析 [ref 9] をX3LYP/def2-TZVPPレベルで行いました.また,RI-SCS-MP2/def2-QZVPPレベル [ref 10, ref 7]での一点計算でエネルギーを求め,分散力も含まれた高精度な相互作用エネルギーを算出しました.計算のうち,構造最適化はFirefly 7.1.G [ref 11] で行い,NBO解析はFireflyに組み込まれたNBO 5.G [ref 12] を用いて行いました.RI-SCS-MP2計算はORCA 2.7.0 [ref 13] を用いて行い,RI-JKとRI-MP2近似を導入し,対応したJK FittingまたはMP2 Fitting補助基底関数を用いて計算しました.
参考文献
- 1) Nagao, Y,; Hirata, T.; Goto, S.; Sano, S.; Kakehi, A.; Iizuka, K.; Shiro, M. J. Am. Chem. Soc.1998, 120, 3104–3110.
- 2) (a) Iwaoka, M.; Takemoto, S.; Okada, M.; Tomoda, S. Chem. lett.2001, 132–133; (b) Iwaoka, M.; Takemoto, S.; Okada, M.; Tomoda, S. Bull. Chem. Soc. Jpn.2002, 75, 1611–1625; (c) Iwaoka, M.; Komatsu, H.; Katsuda, T.; Tomoda, S. J. Am. Chem. Soc.2004, 126, 5309–5317.
- 3) Chein, R.-J.; Corey, E. J. Org. Lett.2010, 12, 132–135.
- 4) (a) Burling, F. T.; Goldstein, B. M. J. Am. Chem. Soc.1992, 114, 2313–2320; (b) Markham G. D.; Bock, C. W. J. Mol. Struct.: THEOCHEM1997, 418, 139–154; (c) Lois, S.; Florès J.-C.; Lère-Porte, J.-P.; Serein-Spirau F.; Moreau, J. J. E.;
Miqueu, K.; Sotiropoulos, J.-M.; Baylère, P.; Tillard, M.; Belin, C. Eur. J. Org. Chem.2007, 4019–4031.
- 5) Bondi, A. J. Phys. Chem.1964, 68, 441–451.
- 6) Xu, X.; Goddard III, W. A. Proc. Natl. Acad. Sci. USA2004, 101, 2673–2677.
- 7) Weigend, F.; Ahlrichs, R. Phys. Chem. Chem. Phys.2005, 7, 3297–3305.
- 8) Zhao, Y.; Truhlar, D. G. J. Chem. Theory Comput.2005, 1, 415–432.
- 9) (a) Foster, J. P.; Weinhold, F. J. Am. Chem. Soc.1980, 102, 7211-7218; (b) Reed A. E.; Weinhold, F. J. Chem. Phys.1983, 78, 4066–4073; (c) Reed, A. E.; Weinstock, R. B.; Weinhold, F. J. Chem. Phys.1985, 83, 735–746.
- 10) Grimme, S. J. Chem. Phys.2003, 118, 9095–9102.
- 11) Granovsky, A. A. Firefly version 7.1.G, http://classic.chem.msu.su/gran/firefly/index.html
- 12) NBO 5.G., Glendening, E. D.; Badenhoop, J. K.; Reed, A. E.; Carpenter, J. E.; Bohmann, J.
A.; Morales, C. M.; Weinhold, F. (Theoretical Chemistry Institute, University of Wisconsin,
Madison, WI, 2004); http://www.chem.wisc.edu/~nbo5/
- 13) Neese, F. ORCA – an ab initio, Density Functional and Semiempirical program package, Version
2.7.0, University of Bonn, 2010. http://www.thch.uni-bonn.de/tc/orca/

