水素化熱の計算
シクロヘキセン,1,3-シクロヘキサジエンおよびベンゼンの水素化は以下の反応式で表されます.
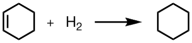 (1)
(1)
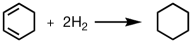 (2)
(2)
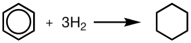 (3)
(3)
これらの反応のエンタルピーΔHが,それぞれの反応の水素化熱になります.それでは様々な汎関数で計算した結果を表1-3にまとめます.
| 方法 | 水素化熱ΔHH [kcal/mol] | 誤差 [kcal/mol] |
|---|---|---|
| 実験値 (ref. 1) | -28.09 | - |
| B3LYP/6-311+G(d,p) | -26.20 | 1.89 |
| B3PW91/6-311+G(d,p) | -28.82 | -0.73 |
| O3LYP/6-311+G(d,p) | -30.02 | -1.95 |
| PBE0/6-311+G(d,p) | -30.90 | -3.81 |
| PBE/TZV(2d,2p) | -27.73 | 0.36 |
| B3PW91/cc-pVTZ | -28.31 | -0.22 |
| B3PW91/6-311+(2df,p) | -28.05 | 0.04 |
| M06-2X/MG3S//B3PW91/6-311+(2df,p) | -29.18 | -0.94 |
| B2PLYP-D/def2-QZVPP//B3PW91/6-311+(2df,p) | -28.95 | -0.86 |
| M06-2X/MG3S//PBE/TZV(2d,2p) | -28.97 | -0.88 |
| B2PLYP-D/def2-QZVPP//PBE/TZV(2d,2p) | -28.81 | -0.72 |
| 方法 | 水素化熱ΔHH [kcal/mol] | 誤差 [kcal/mol] |
|---|---|---|
| 実験値 (ref. 2) | -54.26 | - |
| B3LYP/6-311+G(d,p) | -50.93 | 3.33 |
| B3PW91/6-311+G(d,p) | -56.41 | -2.15 |
| O3LYP/6-311+G(d,p) | -58.65 | -4.39 |
| PBE0/6-311+G(d,p) | -62.54 | -8.28 |
| PBE/TZV(2d,2p) | -53.88 | 0.38 |
| B3PW91/cc-pVTZ | -55.45 | -1.19 |
| B3PW91/6-311+(2df,p) | -54.98 | -0.72 |
| M06-2X/MG3S//B3PW91/6-311+(2df,p) | -56.91 | -2.65 |
| B2PLYP-D/def2-QZVPP//B3PW91/6-311+(2df,p) | -55.90 | -1.64 |
| M06-2X/MG3S//PBE/TZV(2d,2p) | -56.86 | -2.60 |
| B2PLYP-D/def2-QZVPP//PBE/TZV(2d,2p) | -55.67 | -1.41 |
| 方法 | 水素化熱ΔHH [kcal/mol] | 誤差 [kcal/mol] |
|---|---|---|
| 実験値 (ref. 3) | -49.06 | - |
| B3LYP/6-311+G(d,p) | -41.13 | 7.93 |
| B3PW91/6-311+G(d,p) | -49.06 | 0.00 |
| O3LYP/6-311+G(d,p) | -52.36 | -3.30 |
| PBE0/6-311+G(d,p) | -57.93 | -8.87 |
| PBE/TZV(2d,2p) | -46.26 | 2.80 |
| B3PW91/cc-pVTZ | -48.32 | 1.74 |
| B3PW91/6-311+(2df,p) | -46.87 | 2.19 |
| M06-2X/MG3S//B3PW91/6-311+(2df,p) | -49.89 | -0.83 |
| B2PLYP-D/def2-QZVPP//B3PW91/6-311+(2df,p) | -47.26 | 1.80 |
| M06-2X/MG3S//PBE/TZV(2d,2p) | -49.87 | -0.81 |
| B2PLYP-D/def2-QZVPP//PBE/TZV(2d,2p) | -47.07 | 1.99 |
表4に計算した水素化熱と実験値との間に生じた誤差の二乗平均平方根 (RMS) を示します.
| 方法 | RMS |
|---|---|
| B3LYP/6-311+G(d,p) | 5.09 |
| B3PW91/6-311+G(d,p) | 1.31 |
| O3LYP/6-311+G(d,p) | 3.36 |
| PBE0/6-311+G(d,p) | 7.34 |
| PBE/TZV(2d,2p) | 1.64 |
| B3PW91/cc-pVTZ | 1.22 |
| B3PW91/6-311+(2df,p) | 1.33 |
| M06-2X/MG3S//B3PW91/6-311+(2df,p) | 1.69 |
| B2PLYP-D/def2-QZVPP//B3PW91/6-311+(2df,p) | 1.49 |
| M06-2X/MG3S//PBE/TZV(2d,2p) | 1.65 |
| B2PLYP-D/def2-QZVPP//PBE/TZV(2d,2p) | 1.47 |
全体的な傾向としてB3PW91が実験値とよい一致を示しました.GGA汎関数のPBEもなかなか優秀です.
B2PLYP-Dもよい一致を示しています.M06-2Xは1,3-シクロヘキサジエンの水素化熱の見積りがやや悪いようですが,平均すれば比較的よい一致を示しています.このあたりは流石といったところでしょうか.なお,これらの計算では構造最適化をB3PW91で行った場合もPBEで行った場合も同程度の精度であり,DFTとtriple-zetaレベルの基底関数で十分な精度の構造が得られるようです.
一方で,DFT計算のスタンダードであるB3LYPは精度が悪いです.とくにベンゼンの水素化熱では8 kcal/mol近い誤差があります.O3LYPではベンゼンの水素化熱の誤差が改善されて,平均的にはだいぶまともになっています.PBE0はこの種の問題には不適当なようで,1,3-シクロヘキサジエンとベンゼンの水素化熱を8 kcal/mol以上も過大に見積もります.